|
Fibonacci serisi sayıları:0, 1,1,2,3,5,8,13,21,34,55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, … vb. şeklinde devam eder. Her sayı kendisinden önce gelen iki sayının toplamıdır. Bu durumda genel olarak n'inci Fibonacci sayısı F(n) şu şekilde ifade edilir:
-
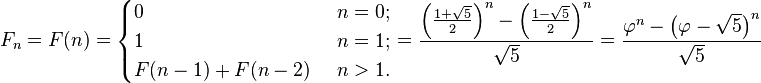 1. end{cases}=frac{left(frac{1+sqrt{5}}{2}right)^n-left(frac{1-sqrt{5}}{2}right)^n}{sqrt{5}}=frac{varphi^n-left(varphi-sqrt{5}right)^n}{sqrt{5}} " />
Fibonacci sayılarının ilginç özellikleri vardır. Mesela n sayısı büyüdükçe iki ardışık Fibonacci sayısının oranı Altın oran'a yani 1.618... e yakınsar.
-
|



