serifedemiral - Sayilar

Genel Bilgiler

7.Sinif Matematik

Paylaş

| More

serifedemiral

Sayılar

Sayma sayılar

Sayma sayılarını boştan farklı bir kümenin elemanlarını azlık veya çokluk yönünden nitelemekten ziyade onların içindeki eleman miktarına göre verilen bir temsilciler kümesi olarak tanımlanır.Temsilcilere verilen isim kanonik temsilci denir.Her sayma sayısı aynı zamanda bir kanonik temsilcidir.Sayma sayılarına sıfırın dahil olmamasının sebebi boş kümenin içinde temsil edcek bir elemanın olmamasıdır.

Doğal sayılar

Doğal sayılar 0'dan başlayarak sonsuza kadar giden sayılardır. Matematikte doğal sayılar kümesi $mathbb N$ ile gösterilir. $mathbb{N} = { 0, 1, 2, 3, 4, 5, 6, 7, ... }$

Doğal sayılar ismi bu sayıların doğada görüp tanıdığımız sayılar olduğu fikrinden ileri gelmektedir.doğal sayılar kümesi "0" ve pozitif tüm sayıların olduğu kümedir N harfi ile gösterilir. Bazı otoritelere göre "0" doğal sayı olarak kabul edilmez.

Tam sayılar

Tam sayılar eksi sonsuzdan artı sonsuza kadar giderler. Yani "0"ın iki yanından sonsuza kadar uzanırlar. Tam sayılar kümesi $mathbb Z$ ile gösterilir.

$mathbb Z = {..., -4, -3, -2, -1, 0, 1, 2, 3, ... }$

POZITIF TAMSAYILAR

Başında "+" işareti bulunan veya bir şey bulunmayan tam sayılar pozitif tamsayılar adını alırlar. Sayı ekseninde (sayı doğrusunda) 0'ın sağ yanında yer alırlar. Tüm sayma sayıları pozitif tam sayılardır. Pozitif tamsayılar kümesi $mathbb Z^{+}$ ile gösterilir ve aşağıdaki gibi tanımlıdır:

$mathbb Z^{+} = { +1, +2, +3, +4, +5... }$

Negatif tamsayılar

Başında "-" işareti olan tam sayılar negatif tamsayılar adını alırlar. Sayı ekseninde 0'ın sol yanında yer alırlar. Negatif tamsayılar kümesi $mathbb Z^{-}$ ile gösterilir. Cebirde çıkarma işlemi bu sayıların diğer tamsayılarla toplanması olarak ifade edilir.

$mathbb Z^{-} = { ..., -3, -2, -1 }$

SIFIR

Sıfır 0 negatif veya pozitif bir tam sayı değildir.bir uzlaşma noktasıdır. Bu iki kümeden herhangi birinde yer almaz. Ancak tamsayılar aşağıdaki gibi de tanımlanabilir:

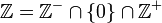
$mathbb Z = mathbb Z^{-} cap { 0 } cap mathbb Z^{+}$

Sıfırın doğal sayı kabul edilmediği (akademik) çevreler azımsanmayacak kadar fazladır. Sıfırı dahil etmeyen çevreler doğal sayılar kümesini $mathbb{N}_{(0)}$ sembolü ile gösterirler, sıfırı dahil eden çevrelerse sıfırın dahil olmadığı sayma sayıları kümesini $mathbb{N}^{+}$ ile gösterirler.

Oranlı sayılar

Oranlı sayılar veya rasyonel sayılar: Tam sayılar kullanılarak oluşturulan oranlara denk gelen büyüklüklere oranlı sayılar denir. Hisseli hesapları kolaylaştırmak için sayı kavramına dahil edilmişlerdir. Tamsayılar üzerindeki bölme işleminin bir genişlemesidir. Oranlı sayıların simgesi $mathbb Q$ dur ve $mathbb Q = { frac{a}{b} | a,b in mathbb Z and b neq 0 }$ olarak tanımlanır. a herhangi bir tamsayı olabilir, ama "b" 0 dışındaki tüm tamsayılardır. Kesirli sayılardır ve artı sonsuzdan eksi sonsuza kadar giderler. $mathbb Q$ 'nün kardinalitesi alef sıfırdır. Yani eleman sayısı doğal sayıların eleman sayısına eşittir. Tüm tam sayılar aynı zamanda oranlı sayılar kümesine üyedir. Bunun nedeni b = 1 alınarak a/b formatına uygun hale getirilebilecek olmalarıdır. lsejflkşsmklşsdvmlşvmdslkvmsdşvldşvmlşvmsdvşömdvldmölşsdkmşlvdmşsdmlvmdsvsklşdnvlksvndslkvnlknsdvklnvsdknlkvdslkvdsnvldlkvnsdklvdnvksdnlkvsdvsd

Oransız sayılar

Oransız sayılar veya İrrasyonel sayılar ise a/b şeklinde yazılamayan sayılardır. Q' kümesi ile gösterilirler. Bu kümenin en bilinen üyesi pi sayısıdır.

Örnek:√2, ∏

Hiç bir oranlı sayı oransız sayılar kümesine dahil değildir. Aynı şekilde hiçbir oransız sayı da oranlı sayılar kümesine dahil değildir.

Gerçek Sayılar

Oransız sayılar kümesi ile oranlı sayılar kümesinin birleşimi gerçek sayılar kümesini oluşturur. Bu kümeye reel sayılar veya gerçel sayılar da denir. Geometride karşılaşılan bazı büyüklüklerin anlamlandırılabilmesi için Klasik Yunan Dönemi'nde, yaygın inanca göre Pisagor ve öğrencileri tarafından sayı kavramına dahil edilmişlerdir. Anlatılanlara göre Pisagor doğadaki tüm büyüklüklerin rasyonel sayılarla ifade edilebileceğini söylemekteydi. Fakat bulduğu hipotenüs eşitliğinin bir sonucu olarak

x 2 = 2

gibi bir değerlerle karşılaştı. Uzun yıllar boyu bu tür sayıların uzun kesirlerle ifade edilebileceğini iddia etti ve göstermeye çalıştıysa da, öğrencilerinden birinin bu gibi sayıların kesinlikle kesirli bir biçimde gösterilemeyeceğini ispat etmesiyle ikna olur ama hayatı boyu bunun bir sır gibi gizlenmesi için çalışır ve doğada gerçek sayıların yeri olmadığını söylemeye devam eder.

Gerçek sayılar, katsayıları tamsayılar ya da rasyonel sayılar olan polinomlar kümesinin çözümlerini göstermek için kullanılırlar. Bu bakımdan gerçek sayılar kümesi, tamsayı katsayılı polinomlar kümesi $mathbb Z[x]$ in bir cisim genişlemesidir.

Gerçek sayılar kümesi $mathbb R$ harfi ile ifade edilir.

Karmaşık sayılar

Tüm cebirsel denklemleri çözebilmek için reel sayılar tekrar genişletilirse karmaşık sayılar veya kompleks sayılar kümesi elde edilir. Karmaşık sayıların sembolü $mathbb C$ dir. Rönesans döneminde gerçekleşen cebirsel denklemlerin çözüm metodlarındaki ilerlemelerin bir uzantısı olarak sayı kavramına eklenmişlerdir. Gerçek olmayan sayılar fikri reel sayılar kümesinde karşılığı olmayan -1 sayısının karekökünden gelmektedir. Bu sayı "i" sembolü ile gösterilir ve karesi -1 olarak kabul edilir.

Sınıflama özeti

Matematiksel notasyonda yukarıdaki bütün semboller büyük harfle ve kalın olarak yazılır.

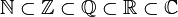
$mathbb{N}submathbb{Z}submathbb{Q}submathbb{R}submathbb{C}$

Bir tablo olarak sayılar için şöyle sınıflandırma yapılabilir:

$mathbb{C} mbox{ Karmasik} begin{cases} mathbb{R} & mbox{Gercel} begin{cases} mathbb{Q} & mbox{Rasyonel} begin{cases} mathbb{Z} & mbox{Tam sayilar} begin{cases} mathbb{N} & mbox{Dogal} & mbox{Negatif tamsayilar} end{cases} & mbox{Oranli} end{cases} & mbox{Irrasyonel} end{cases} & mbox{Sanal} end{cases}$

8.Sinif Matematik

hi5 Mouse Cursors
Bu web sitesi ücretsiz olarak Bedava-Sitem.com ile oluşturulmuştur. Siz de kendi web sitenizi kurmak ister misiniz?

Ücretsiz kaydol